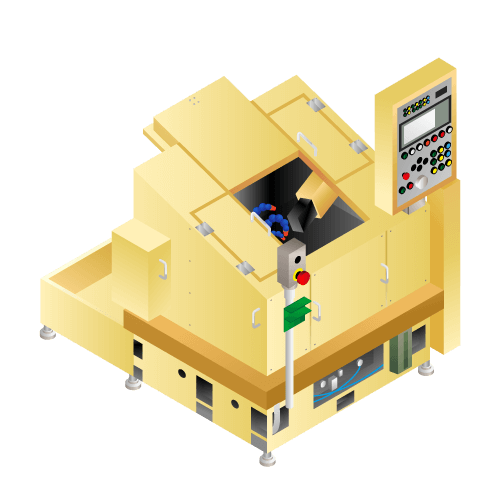
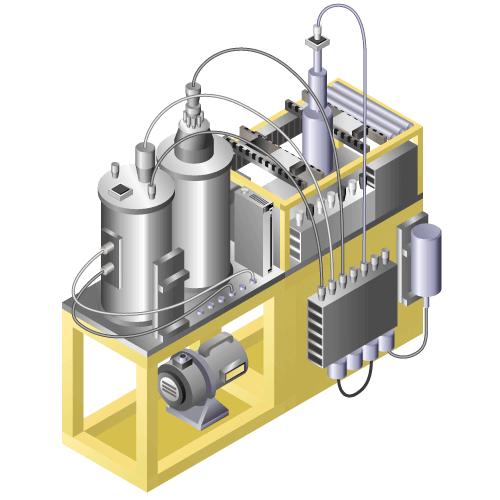
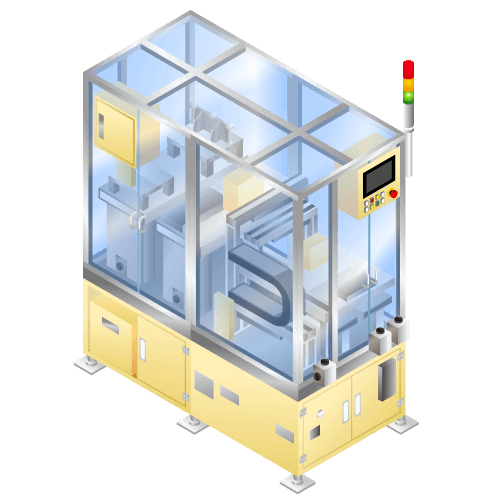
Complied matters
18650 Cylindrical lithium-ion batteries are very competitive and sales price is in a tough situation. Therefore customer needs to cut down cost of equipments to get ahead of the competition. In this line, processes with high difficulty level were manufactured in Japan and the others were designed and manufactured in our Chinese factory. We realized lines combined with Japanese quality and merit of cost in China. So we could hold down investment of customer at minimum with maintenance of quality and rate of operation.
Technology used
-

Battery Material Handling
Some materials used for secondary batteries, such as lithium-ion etc., need special handling. The electrode should be handled at high speed without causing damage to fragile active material. In the electrolyte, special consideration is required for prevention of the generation of precipitation and corrosion gas. We have extensive experience in dealing with such battery material.
See machines using this technology > -
The Machine on Battery Material Handling
-
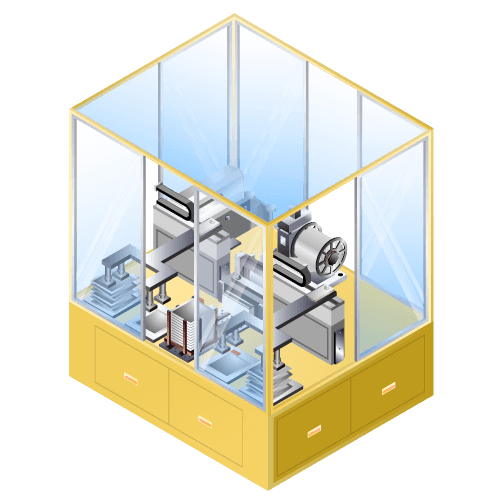
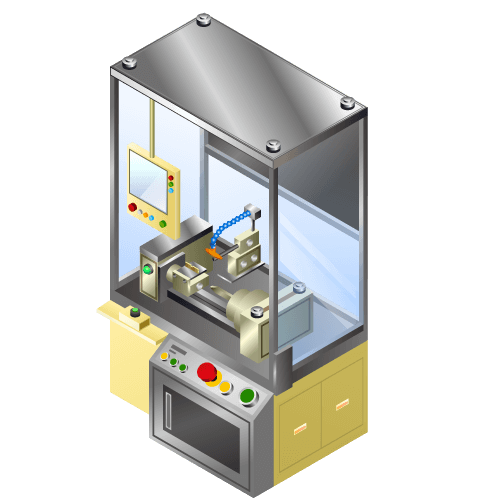
Roll press for lithium-ion secondary batteries etc.
Machine to increase density of electrode material by pressing positive electrode or negative electrode of lithium-ion etc. with roller continuously.
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Sheet to Roll Optical Film Adhering Machine
Machine to adhere 1 sq. meter sheet-shaped film or more with a clearance of 0.5mm to roll film with a width of 1meter or more continuously. Adhered roll films are cut to make sheet-shaped films and are stored.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
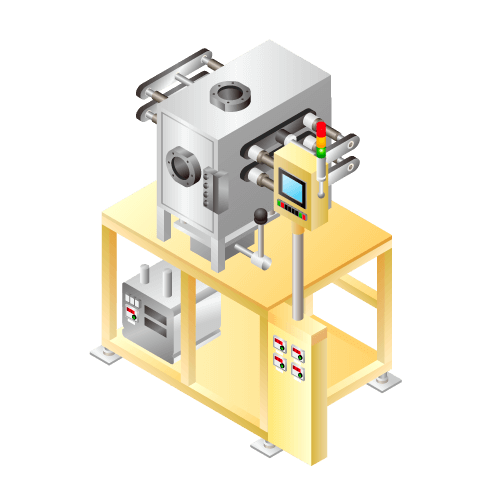
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc. for small-quantity production
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc. This machine requires manual operation and is intended for small-quantity production.
-
Electrode cutting machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to cut positive or negative electrode of lithium-ion batteries etc. from original roll to batteries size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate forming (cup forming) machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries etc. Machine including hand working for small-quantity production.
-
Laminate outer shape stamping machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to stamp outer shape of embossed laminate film to roll up electrodes for items such as lithium-ion batteries etc. and to make them the prescribed size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to seal laminate film with rolled up electrodes such as lithium-ion batteries, etc. with heater block. This machine requires manual operation and is intended for small-quantity production.
-
Electrolytic injection machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries etc. This machine requires manual operation and is intended for small-quantity production.
-
Degassing and sealing machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to discharge gas produced at the first charging in manufacturing process of lithium-ion batteries etc. from batteries cell and to reseal.
-
Laminate blank space cutting machine for lithium-ion secondary batteries etc. for small-quantity production
Jig to cut and remove margin section for accumulated gas of laminate cell of lithium-ion battery etc. Jig for manual operation and is intended for small-quantity production.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
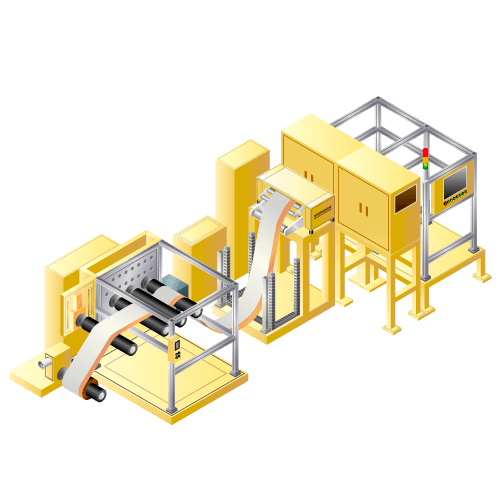
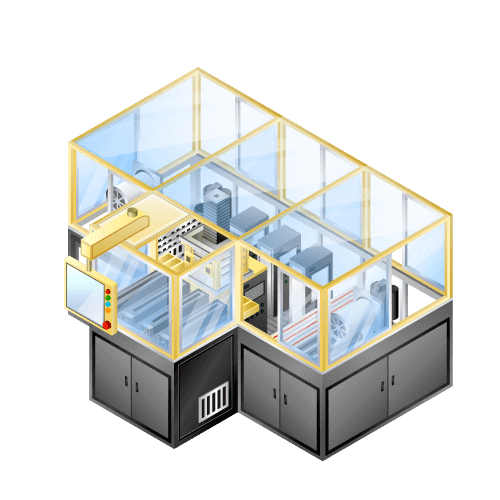
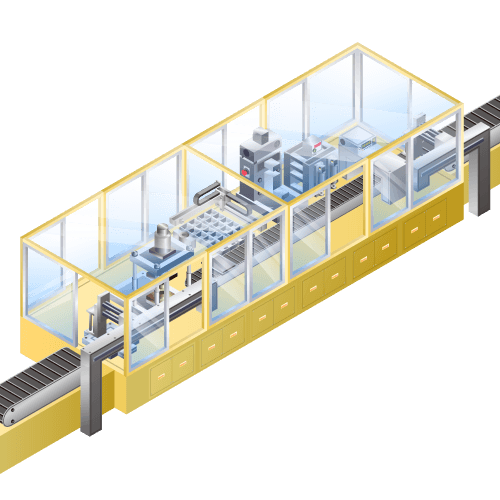
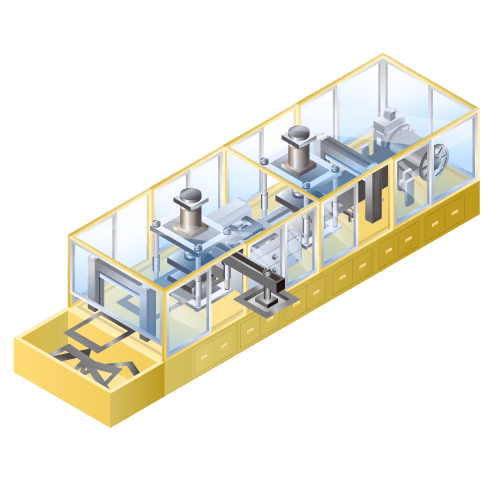
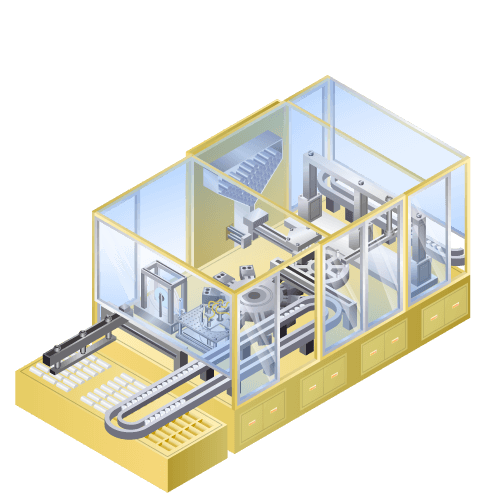
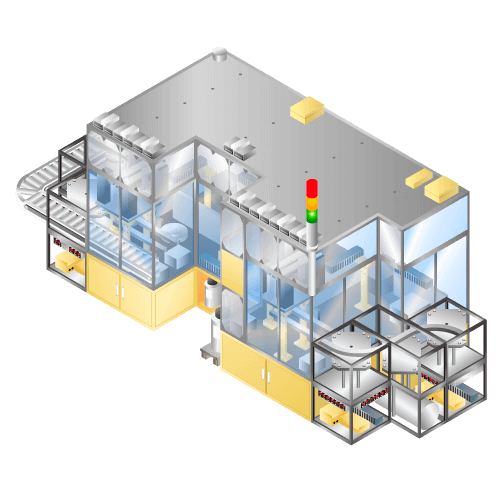
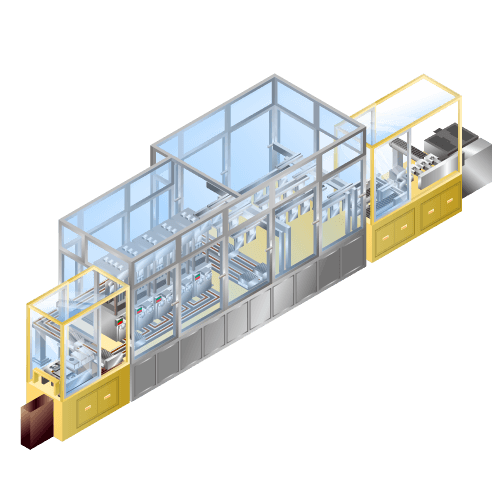
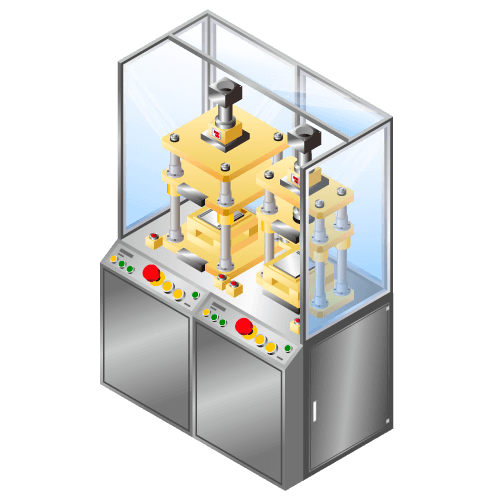
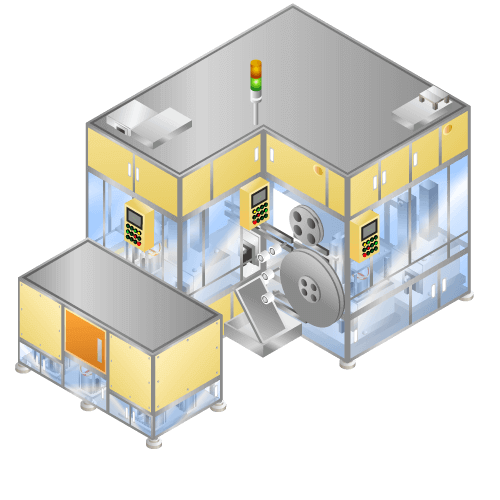
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Cam Unit
If construct machine with the view to tact time less than 1 second with cylinder or AC servo actuator, it is difficult to synchronize or it may be impossible to maintain stable condition for long term even if keeps good condition when installed new machine. Then, cylinder reaches end of its running distance in a short term, therefore it has a short maintenance cycle. In machine constructed cam mechanism, it is able to settle such problem because all driving is held by minimal motor.
See machines using this technology > -
The Machine on Cam Unit
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Mounting and base
Building a strong mounting and base for machinery is important for maintaining stability for the long term. A strong mounting and base also shortens the start-up time by minimizing accuracy deviation to transfer and transport mechanisms. Generally, we have eliminated the use of aluminum frames. We construct stable bases using thick square logs and a substantial base for the can manufacturing process. For various requirements, we do annealing and use a mount with additional accuracy.
See machines using this technology > -
The Machine on Mounting and base
-
Roll press for lithium-ion secondary batteries etc.
Machine to increase density of electrode material by pressing positive electrode or negative electrode of lithium-ion etc. with roller continuously.
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Probe Pin Processing Machine
Machine to give sharply-angled taper processing to cylindrical metallic material with diameter of 0.1mm or less.
-
Sheet to Roll Optical Film Adhering Machine
Machine to adhere 1 sq. meter sheet-shaped film or more with a clearance of 0.5mm to roll film with a width of 1meter or more continuously. Adhered roll films are cut to make sheet-shaped films and are stored.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
Laminating machine with alignment function for film
Machine to apply heat laminate to each supplied film roll with heated roller. Normally, in case of laminating each film roll, apply only width direction by EPC etc, preventing position gap. However, it is able to adjust the position of not only the width direction but also the flow direction by controlling the amount of both feeds.
-
Automobile security parts assembly
Machine to assemble more than 10 different parts in resin parts with diameter of approx. 50mm. The parts used for each product type are different, therefore machine has the function of selecting parts used automatically with change of type.
-
Automobile plumbing components
Assembly machine for automobile parts. Machine to assemble resin parts including laser welding, check air tightness and flow volume.
-
Seal material coating applicator (with course correcting function)
Machine to have correct seal material application imperviously to work variability by correction of application trajectory with measuring work shape. High performance application machine including material heating function, pneumatic transportation of high viscosity material, UV curing process, inspection process after application and data collection function.
-
Piston ring groove processing machine
Machine to groove for "piston ring" for fixing to piston used in internal combustion.
-
Transfer machine (processing machine for several processes)
Machine to process 5 processes such as boring, grooving and C side processing etc. with transporting work on a separate station in order. Some processes employ CNC control to get high accuracy processing.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Vacuum
We have substantial experience not only simple vacuum chamber and furnace but also mechanism with operation process in vacuum chamber and devices for liquid application. We have also immense knowledge of special vacuum equipment such as vacuum pump, piping and valve etc. and parts.
See machines using this technology > -
The Machine on Vacuum
-
Chemical Injection Machine
Machine to inject chemicals into a special container without air bubbles quickly and accurately.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Electrolytic injection machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries etc. This machine requires manual operation and is intended for small-quantity production.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Precise positioning
We have technology and experience to realize alignment system with high cost performance according to needs such as mechanism positioning and image processing. To maintain accuracy for the long term, we realize not only camera or positioning table but also precise positioning including design of mounting.
See machines using this technology > -
The Machine on Precise positioning
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Sheet to Roll Optical Film Adhering Machine
Machine to adhere 1 sq. meter sheet-shaped film or more with a clearance of 0.5mm to roll film with a width of 1meter or more continuously. Adhered roll films are cut to make sheet-shaped films and are stored.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
Laminating machine with alignment function for film
Machine to apply heat laminate to each supplied film roll with heated roller. Normally, in case of laminating each film roll, apply only width direction by EPC etc, preventing position gap. However, it is able to adjust the position of not only the width direction but also the flow direction by controlling the amount of both feeds.
-
Automobile security parts assembly
Machine to assemble more than 10 different parts in resin parts with diameter of approx. 50mm. The parts used for each product type are different, therefore machine has the function of selecting parts used automatically with change of type.
-
Transfer machine (processing machine for several processes)
Machine to process 5 processes such as boring, grooving and C side processing etc. with transporting work on a separate station in order. Some processes employ CNC control to get high accuracy processing.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Laser welding
We have knowledge and result of various laser such as CO2,YAG,LED,Fiber etc. according to individual needs for example laser welding of thin foil of battery etc., welding of throttle case and lid, resin welding instead of metal etc. We suggest the most suitable welding method according to spec and select welding machine. We accept welding test with sample.
See machines using this technology > -
The Machine on Laser welding
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Press
We have technology and experience to respond to various types of press such as air, hydraulic pressure and servo etc. We have wide range of results from hand press of test production level to machine to produce products with high accuracy and high quality controlling speed with servomotor and torque.
See machines using this technology > -
The Machine on Press
-
Roll press for lithium-ion secondary batteries etc.
Machine to increase density of electrode material by pressing positive electrode or negative electrode of lithium-ion etc. with roller continuously.
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Electrode cutting machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to cut positive or negative electrode of lithium-ion batteries etc. from original roll to batteries size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate forming (cup forming) machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries etc. Machine including hand working for small-quantity production.
-
Laminate outer shape stamping machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to stamp outer shape of embossed laminate film to roll up electrodes for items such as lithium-ion batteries etc. and to make them the prescribed size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to seal laminate film with rolled up electrodes such as lithium-ion batteries, etc. with heater block. This machine requires manual operation and is intended for small-quantity production.
-
Degassing and sealing machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to discharge gas produced at the first charging in manufacturing process of lithium-ion batteries etc. from batteries cell and to reseal.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Dimension measurement
Respond to dimension measurement with various methods using laser displacement gauge, image processing equipment, contact and non-contact sensor etc. In production machine, it is impossible to measure correct dimension with only measuring equipment. For this reason, we keep accuracy in a comprehensive manner including vibration of mounting etc.
See machines using this technology > -
The Machine on Dimension measurement
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Automobile plumbing components
Assembly machine for automobile parts. Machine to assemble resin parts including laser welding, check air tightness and flow volume.
-
Seal material coating applicator (with course correcting function)
Machine to have correct seal material application imperviously to work variability by correction of application trajectory with measuring work shape. High performance application machine including material heating function, pneumatic transportation of high viscosity material, UV curing process, inspection process after application and data collection function.
-
Piston ring groove processing machine
Machine to groove for "piston ring" for fixing to piston used in internal combustion.
-
Transfer machine (processing machine for several processes)
Machine to process 5 processes such as boring, grooving and C side processing etc. with transporting work on a separate station in order. Some processes employ CNC control to get high accuracy processing.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Resistance welding
The quality of resistance welding with production machine concerned, the correctness has a huge effect on loading to work. In view of such condition, we suggest material of object, the most suitable welding method according to spec and select welding machine. We accept welding test with sample.
See machines using this technology > -
The Machine on Resistance welding
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Image processing
We have various experience of image processing such as positioning, missing part and scratch etc. Respond to advanced image processing by the combination of the most suitable camera, lighting and processing device in response to shape of an object, accuracy and tact. Then it is also respond to continuous image processing of long object using licenser camera.
See machines using this technology > -
The Machine on Image processing
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Probe Pin Processing Machine
Machine to give sharply-angled taper processing to cylindrical metallic material with diameter of 0.1mm or less.
-
Compact Sensor Assembly Machine
Machine to assemble compact sensors with a size of a few millimeters
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Automobile security parts assembly
Machine to assemble more than 10 different parts in resin parts with diameter of approx. 50mm. The parts used for each product type are different, therefore machine has the function of selecting parts used automatically with change of type.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Improving of assembly accuracy
We have been working processing machines that high accuracy is required since the time of founding. For this reason, we have culture to assemble machine with improving accuracy like processing machine assembly for assembly other than processing machine, too. These machine assembled with improving accuracy is possible to maintain accuracy for long term.
See machines using this technology > -
The Machine on Improving of assembly accuracy
-
Roll press for lithium-ion secondary batteries etc.
Machine to increase density of electrode material by pressing positive electrode or negative electrode of lithium-ion etc. with roller continuously.
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Compact Sensor Assembly Machine
Machine to assemble compact sensors with a size of a few millimeters
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
Electrode cutting machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to cut positive or negative electrode of lithium-ion batteries etc. from original roll to batteries size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate forming (cup forming) machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries etc. Machine including hand working for small-quantity production.
-
Laminate outer shape stamping machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to stamp outer shape of embossed laminate film to roll up electrodes for items such as lithium-ion batteries etc. and to make them the prescribed size. This machine requires manual operation and is intended for small-quantity production.
-
Automobile security parts assembly
Machine to assemble more than 10 different parts in resin parts with diameter of approx. 50mm. The parts used for each product type are different, therefore machine has the function of selecting parts used automatically with change of type.
-
Automobile plumbing components
Assembly machine for automobile parts. Machine to assemble resin parts including laser welding, check air tightness and flow volume.
-
Seal material coating applicator (with course correcting function)
Machine to have correct seal material application imperviously to work variability by correction of application trajectory with measuring work shape. High performance application machine including material heating function, pneumatic transportation of high viscosity material, UV curing process, inspection process after application and data collection function.
-
Piston ring groove processing machine
Machine to groove for "piston ring" for fixing to piston used in internal combustion.
-
Transfer machine (processing machine for several processes)
Machine to process 5 processes such as boring, grooving and C side processing etc. with transporting work on a separate station in order. Some processes employ CNC control to get high accuracy processing.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Wiring technology
We wire in consideration of visual effects and stable use for the long term. We give importance to minimalize stress at operation and selection of the most suitable wiring materials.
See machines using this technology > -
The Machine on Wiring technology
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Compact Sensor Assembly Machine
Machine to assemble compact sensors with a size of a few millimeters
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Twin fluid washing machine (catalog sales)
Washing machine which has the characteristics of machine cost and running cost reduction.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
Laminating machine with alignment function for film
Machine to apply heat laminate to each supplied film roll with heated roller. Normally, in case of laminating each film roll, apply only width direction by EPC etc, preventing position gap. However, it is able to adjust the position of not only the width direction but also the flow direction by controlling the amount of both feeds.
-
Automobile security parts assembly
Machine to assemble more than 10 different parts in resin parts with diameter of approx. 50mm. The parts used for each product type are different, therefore machine has the function of selecting parts used automatically with change of type.
-
Automobile plumbing components
Assembly machine for automobile parts. Machine to assemble resin parts including laser welding, check air tightness and flow volume.
-
Brush washing machine
Machine to take out engine parts aligned on pallet one by one automatically and remove contamination generated in processing by special brush pouring wash solution in washing bath. After washing, blow solution and discharge parts to designated place of pallet.
-
Seal material coating applicator (with course correcting function)
Machine to have correct seal material application imperviously to work variability by correction of application trajectory with measuring work shape. High performance application machine including material heating function, pneumatic transportation of high viscosity material, UV curing process, inspection process after application and data collection function.
-
Piston ring groove processing machine
Machine to groove for "piston ring" for fixing to piston used in internal combustion.
-
Transfer machine (processing machine for several processes)
Machine to process 5 processes such as boring, grooving and C side processing etc. with transporting work on a separate station in order. Some processes employ CNC control to get high accuracy processing.
-
Liquid crystal injection machine
Machine to inject liquid crystal into LCD one by one under vacuum after drying LCD input by magazine in a vacuum.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Countermeasures against Static Electricity (ESD)
Work has a damaging effect by static electricity and disturb stability of film transportation by static electricity. Therefore we need to have technology to stop static generation and remove generated static electricity. Almost all static electricity generated in machine is caused by peel electrification or frictional electrification. We design to make every effort to avoid these electrifications and construct effective neutralization method against generated static electricity by multiple measures of structure and neutralization apparatus.
See machines using this technology > -
The Machine on Countermeasures against Static Electricity (ESD)
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
Sheet to Roll Optical Film Adhering Machine
Machine to adhere 1 sq. meter sheet-shaped film or more with a clearance of 0.5mm to roll film with a width of 1meter or more continuously. Adhered roll films are cut to make sheet-shaped films and are stored.
-
Large size glass carrier machine
Loading machine to take out thin glass with size of 2000mm square or more from storage and transport.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
Single wafer processing film adhering machine
Machine to apply two types of single wafer (sheet shaped) films automatically with a high degree of accuracy without scratches or air bubbles. Each film has a protection film and separator (mold releasing film), which are removed automatically while feeding.
-
-

Dry Room
In the manufacturing of items which are susceptible to moisture such as lithium-ion batteries an ultra low humidity environment is required. The use of normal actuators in such an environment, lubricants do not have the same effect, so special care is required. We also need to take adequate measures against static electricity due to the low humidity environment. We have measures in place which can be used according to the required level of humidity.
See machines using this technology > -
The Machine on Dry Room
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc. for small-quantity production
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc. This machine requires manual operation and is intended for small-quantity production.
-
Laminate forming (cup forming) machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries etc. Machine including hand working for small-quantity production.
-
Laminate outer shape stamping machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to stamp outer shape of embossed laminate film to roll up electrodes for items such as lithium-ion batteries etc. and to make them the prescribed size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to seal laminate film with rolled up electrodes such as lithium-ion batteries, etc. with heater block. This machine requires manual operation and is intended for small-quantity production.
-
Electrolytic injection machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries etc. This machine requires manual operation and is intended for small-quantity production.
-
Degassing and sealing machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to discharge gas produced at the first charging in manufacturing process of lithium-ion batteries etc. from batteries cell and to reseal.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Measure for explosion protection
Countermeasure for explosion protection may be needed for machine using solvent. We have technology and experience in various level of explosion protection for example more safety explosion protection and pressure tight explosion protection etc.
See machines using this technology > -
The Machine on Measure for explosion protection
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Electrolytic injection machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries etc. This machine requires manual operation and is intended for small-quantity production.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-
-

Respond to keep clean condition of battery installation
With a normal clean room, it is possible to protect against contamination with a size of 0.5μm. The size of contamination for battery manufacturing is different. If you set the cleaning level to the same level as a semiconductor facility, it is an insufficient level for battery manufacturing and will contribute to higher costs needlessly. We have the knowledge, technology and experience to keep clean condition of battery manufacturing installations and clear them from contamination and set the cleanliness of the facility to required levels.
See machines using this technology > -
The Machine on Respond to keep clean condition of battery installation
-
Electrode cutting machine for lithium-ion secondary batteries etc.
Machine to cut positive electrode or negative electrode of lithium-ion batteries etc. from original roll to batteries size.
-
Laminating machine for lithium-ion secondary batteries etc.
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy and high speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc.
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc.
-
Laminate forming machine for lithium-ion secondary batteries etc.
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries, etc.
-
Jerry-roll (JR) insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert jerry-roll and bottom insulator to external can of cylindrical lithium-ion batteries etc.
-
Swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to swage external can of cylindrical lithium-ion batteries etc.
-
Negative-electrode welding, CP insertion and TP insertion machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert center pin after welding negative electrode in manufacturing process of lithium-ion batteries, etc. and to insert punched out top insulator for later process.
-
Machine to place groove for cylindrical (18650) lithium-ion secondary batteries etc.
Used in the manufacturing process of items such as lithium-ion batteries, etc.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc.
Machine to seal laminate film which rolled up electrodes such as lithium-ion batteries, etc. with heater block.
-
Injection machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in the manufacturing process of items such as lithium-ion batteries, etc. Developed to shorten the impregnation time by application of pressure in addition to vacuum immersion.
-
Electrolytic injection machine for lithium-ion secondary batteries etc.
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries, etc.
-
Sealing port laser-welding machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to insert sealing port and positive electrode tab to external can after welding by laser in the manufacturing process of items such as lithium-ion batteries, etc.
-
Sealing port swaging machine for cylindrical (18650) lithium-ion secondary batteries etc.
Machine to press and swage external can after being supplied the appropriate cell by insertion sealing port in the manufacturing process of lithium-ion batteries, etc.
-
Laminating machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to pile up positive electrode or negative electrode of lithium-ion batteries and separator in sequence with high accuracy. Unlike the case of production machines, this machine has the priority of machine cost over processing speed.
-
TAB ultrasonic welder for lithium-ion secondary batteries etc. for small-quantity production
Machine to weld collecting tab to electrodes of lithium-ion batteries, etc. This machine requires manual operation and is intended for small-quantity production.
-
Electrode cutting machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to cut positive or negative electrode of lithium-ion batteries etc. from original roll to batteries size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate forming (cup forming) machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to get depression for placing electrodes by embossing laminate film to make packing for rolling up electrodes such as lithium-ion batteries etc. Machine including hand working for small-quantity production.
-
Laminate outer shape stamping machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to stamp outer shape of embossed laminate film to roll up electrodes for items such as lithium-ion batteries etc. and to make them the prescribed size. This machine requires manual operation and is intended for small-quantity production.
-
Laminate three sided heat seal machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to seal laminate film with rolled up electrodes such as lithium-ion batteries, etc. with heater block. This machine requires manual operation and is intended for small-quantity production.
-
Electrolytic injection machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to inject electrolyte into cell in manufacturing process such as lithium-ion batteries etc. This machine requires manual operation and is intended for small-quantity production.
-
Degassing and sealing machine for lithium-ion secondary batteries etc. for small-quantity production
Machine to discharge gas produced at the first charging in manufacturing process of lithium-ion batteries etc. from batteries cell and to reseal.
-
Laminating machine (zigzag system) for layered lithium-ion batteries etc.
Machine to layer electrode of layered lithium-ion batteries etc.. System to insert positive and negative electrode to separator folded in a zig-zag manner alternately.
-
18650 cylindrical lithium-ion batteries etc. assembly line
18650 cylindrical lithium-ion batteries assembly line, consistent line from insertion of jerry roll to crimp.
-